Student: Poorbayan Das
Committee: Dr. Jeonglae Kim
Abstract:
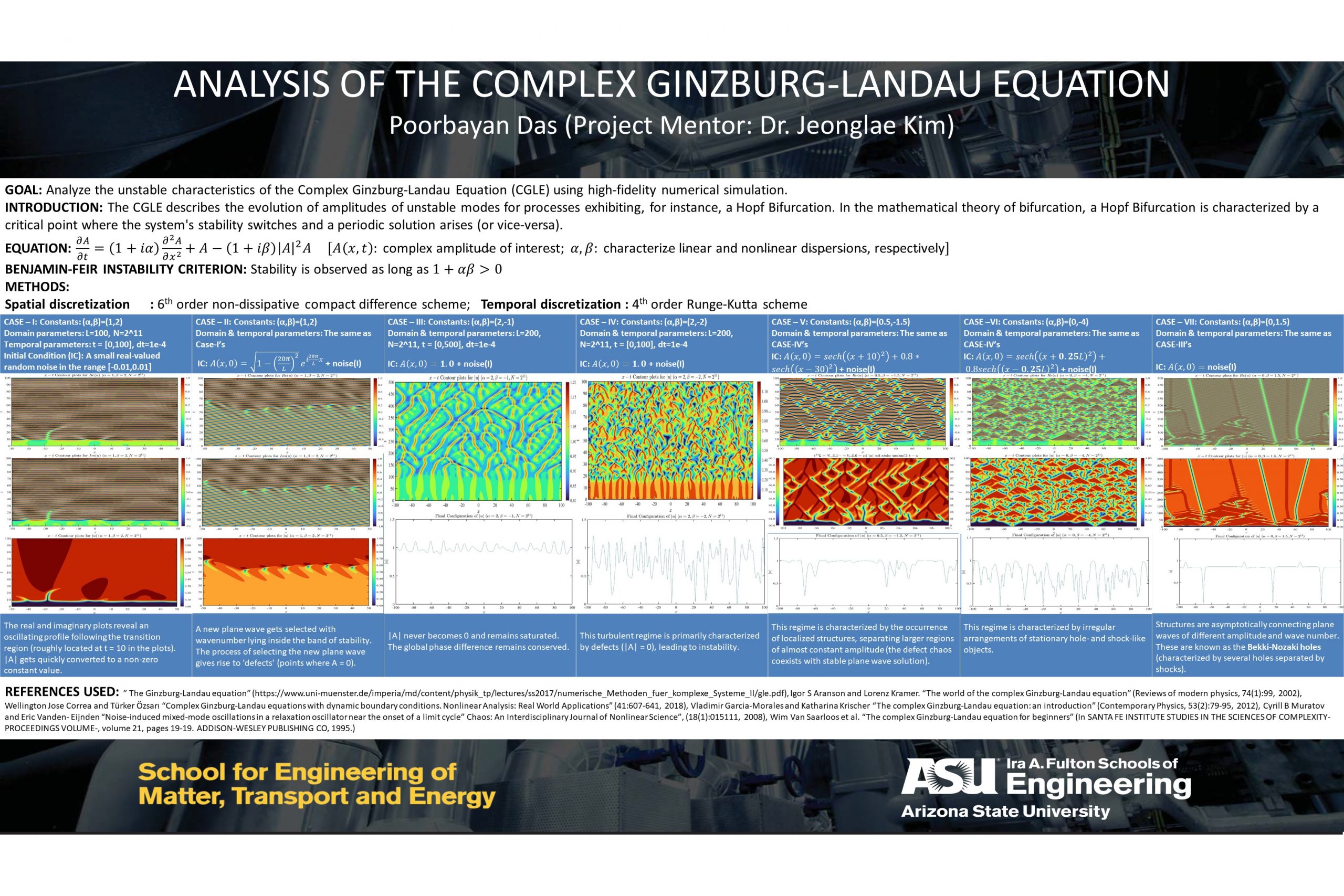
The Complex Ginzburg-Landau equation is one of the most studied nonlinear equations in the physics community. It describes a vast variety of phenomena from nonlinear waves to second-order phase transitions, from superconductivity, super-fluidity, and Bose-Einstein condensation to liquid crystals and strings in field theory. The aim of this project is to simulate the well-known 1-dimensional Complex Ginzburg-Landau Equation (CGLE) numerically using 6th-order Non-Dissipative Compact Difference Spatial Scheme and 4th-order Runge-Kutta Temporal Difference Scheme. The equation is analyzed initially within the stability limit and then further analysis is done on its unstable characteristics, most notably, the intermittent characteristics (stable solution intertwined with unstable defects and shocks).
Zoom Room: https://asu.zoom.us/j/8514851990
Presentation Time: 12:00-1:00 PM (Arizona Time)